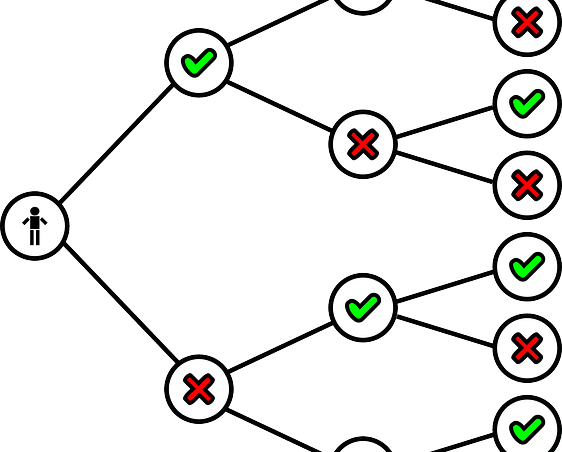
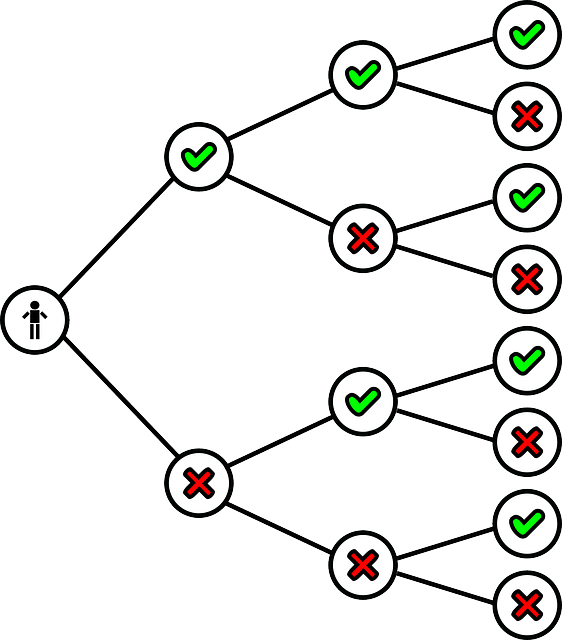
Firstly, Binary Tree is a kind of Data Structure that contain maximum of two children i.e left child and right child. Let us take a look at some of its properties.
Nodes in Binary Tree
- Root node : A first node or the main node is the root node in binary tree.
- Parent node: A node with one or more child nodes is the parent node.
- Child node: A node with one parent node is known as the child node.
- Siblings : Siblings have the same parent node.
- Internal node: It has atleast one child node. Moreover, every non-leaf node is an internal node.
- Leaf node: The last node is known as the leaf node.
Properties of Binary Tree
- Firstly, Maximum number of nodes in a binary tree of height ‘h’ is 2h-1.
- Secondly, When there exists l leaf nodes, then it has atleast l+1 levels.
- Thirdly, a binary tree of node n can have n+1 null references.
Degree of a binary tree means how many total children it has. In addition, height of a binary tree means the total number of edges from leaf to that the root node in the longest path.
Binary Search Tree
Binary Search Tree(BST) is a special kind of binary tree with properties as follows:
- Firstly, if the value is less than the root node, it belongs to the left subtree.
- Secondly, if the value is greater than the root node, it belongs to the right subtree.
Steps to create a BST
- Create new node with a value.
- Check whether the tree is empty or not.
- Moreover, If the tree is empty, set root to the new node.
- In addition, If it is not empty, check if the given key value is smaller or larger than the root node.
- If value is smaller, place it in the left subtree.
- If value is larger, place it in the right subtree.
- Lastly, repeat this steps until we reach leaf node.
Applications of BST
BST can be use in network applications and virtual memory access.
A-V-L Tree
Adelson, Velskii, and Landi (AVL) Tree is a self balancing BST where the difference between heights of the left and right subtree is not more than one for all nodes. Moreover, we need to find the balance factor to create AVL Tree.
To find balance factor, we subtract right level value from the left level value. In addition, it can only have values like -1, 0 or 1. For instance, if balance factor is equal to -2, that node is a critical node.
There are four types of rotation in AVL Tree:
- Left Left (L L) Rotation
- Right Right (R R) Rotation
- Left Right (LR) Rotation
- Right Left (R L) Rotation
Conclusion
In conclusion, we have learnt that Binary Tree is a kind of Data Structure that contain maximum of two children i.e left child and right child. We have also learnt about various nodes i.e root node, internal node, parent node, child node and leaf node.
Moreover, we have seen some of its properties. Maximum number of nodes in a this tree of height ‘h’ is 2h-1. When there exists l leaf nodes, then it has atleast l+1 levels. Degree of a this tree means how many total children it has.
We have also learnt about (BST) and Adelson, Velskii, and Landi (AVL) Tree. Adelson, Velskii, and Landi (AVL) Tree is a self balancing BST where the difference between heights of the left and right subtree is not more than one for all nodes.